一體化電機模組是機器人領域的重要發展方向,它省去了中間傳動部件,將電機和減速器集成為一個模組整體,機器人的動力傳動系統結構得以簡化,使得動力傳動系統更緊湊。
傳動效率是機器人一體化電機模組的重要指標,較高的傳動效率不僅可以減小動力組件的體積和質量,而且還能降低整機的能耗,增加待機時間。
另外,在關節機器人應用領域,很多場合通過檢測電機電流從而對外力進行估計,減速器傳動效率越高,則減速器的機械阻抗就越小,外力和電機之間的力傳遞就越透明。因此,高傳動效率的減速器,能實現機器人關節更高精度的基于電機電流環的外力感知。
本文主要針對一體化電機模組中的減速器進行傳動效率計算和優化分析,現有齒輪減速器效率優化方法過于復雜,需要進行復雜的前處理,不便于在設計初期快速確定減速器關鍵參數。本文基于傳動效率精確計算公式,推導了 3K 行星齒輪系統精確的效率計算公式,并提供了一種通過調整齒輪組中心距和齒輪變位系數來獲得該減速器最高嚙合效率的方法,只需要輸入齒輪模數、各齒輪齒數、齒頂高系數和標準壓力角,便可以計算得到效率最高時的減速器關鍵參數(最優中心距和最優變位系數),有助于設計者在設計初期快速確定減速器齒輪系統的關鍵參數。
1、一體化電機模組機械設計
本文所研究的一體化電機模組結構如圖 1 所示,包括減速器、殼體、電機、編碼器。電機轉子通過平鍵與減速器太陽輪連接,將動力傳遞到減速器輸入端,編碼器用于獲取電機轉子位置,外部驅動器(未圖示)用于對該一體化電機模組進行控制。該模組將電機和減速器高度集成為模組形式,可以顯著減小傳動系統的體積和質量,有利于提升機器人系統的功率密度。
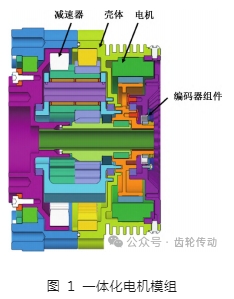
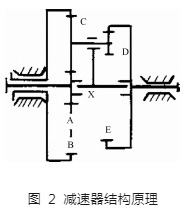
減速器原理如圖 2 所示,為 3K 型減速器,齒輪 A 為輸入端太陽輪,齒輪 C 為一級行星齒輪,齒輪 B為一級內齒圈,齒輪 D 為二級行星齒輪,齒輪 E 為二級內齒圈(動力輸出齒圈)。該類型減速器可以在有限的空間實現較大速比傳動,相比其他類型的齒輪減速器,能夠有效減小模組的體積和質量,從而提高模組的功率密度。
2、減速器嚙合效率精確計算
目前計算減速器嚙合效率的方法主要有以下兩種:
(1)日本學者兩角宗晴公式:
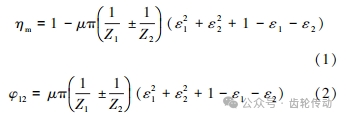
式中:ηm 是嚙合效率;μ 是摩擦系數;Z1,Z2 分別是齒輪 1 和齒輪 2 的齒數;ε1,ε2 分別是嚙入重合度和嚙出重合度;φ12 為齒輪副的嚙合效率損失。
(2)蘇聯學者庫德略采夫公式:
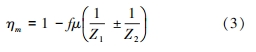
式中:f 是與齒輪齒頂高系數 h∗a 相關的系數;當 h∗a ≤m 時,f= 2. 3,當 h∗a=(1. 0~1. 8)m 時,f = 3. 1,m 為齒輪模數。
兩角宗晴的公式較為精確,而我國工程技術人員多采用庫德略采夫的公式。根據庫德略采夫的公式,齒輪嚙合效率只跟摩擦系數 μ、兩個齒輪的齒數 Z1 和 Z2 、齒頂高系數 h∗a 有關,而實際上,不同的中心距及不同的齒輪變位系數也會影響齒輪嚙合效率。
本文主要基于兩角宗晴的嚙合效率公式,詳細推導出齒輪嚙合效率與齒輪中心距和齒輪變位系數的關系,并給出最高嚙合效率對應的最優齒輪中心距和最優齒輪變位系數確定的方法。
本文采用的 3K 行星減速器齒輪系的嚙合效率:

式中:ηBAE是 3K 行星減速器齒輪系的嚙合效率;iBAE 為齒輪 B 固定、齒輪 A 輸入、齒輪 E 輸出的減速比;iXAB為支架 X 固定、為齒輪 A 輸入、齒輪 B 輸出的減速比;iXEB為支架 X 固定、齒輪 E 輸入、齒輪 B 輸出的減速比;ZA ,ZB ,ZC ,ZD ,ZE 分別為齒輪 A,B,C,D,E 的齒數;φ X EB 為支架 X 固定、齒輪 E 輸入、齒輪 B 輸出時傳動機構中各齒輪副嚙合損失系數之和。
減速器各齒輪齒數由傳動比需求和結構限制確定后,減速器齒輪系的嚙合效率中唯一的未知數為式(4)中的 φ XEB ,其計算公式 :
式中:φXBC 為支架 X 固定、齒輪 B 輸入、齒輪 C 輸出時齒輪副嚙合損失系數;φ X DE 為支架 X 固定、齒輪 D 輸入、齒輪 E 輸出時齒輪副嚙合損失系數。
根據式(2),式(8)中齒輪副嚙合損失系數 φ XBC 和 φXDE 的計算公式:
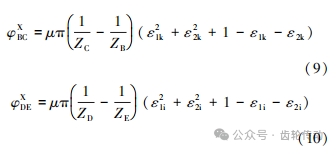
式中:ε1k 為齒輪 B、齒輪 C 嚙入重合度;ε2k 是齒輪 B、齒輪 C 嚙出重合度;ε1i 為齒輪 D、齒輪 E 嚙入重合度;ε2i 是齒輪 D、齒輪 E 嚙出重合度。
φXBC 和 φXDE 為兩對齒輪副嚙合損失系數,其計算方法是一樣的,下面以 φXBC 的計算為例進行公式推導,φXDE 公式推導方法跟 φXBC 相同。
式(9)中齒輪 B、齒輪 C 嚙入重合度 ε1k,齒輪B、齒輪 C 嚙出重合度 ε2k 計算公式如下:

式中:αk 是齒輪 B 和齒輪 C 的嚙合壓力角;αB 是齒輪 B 齒頂壓力角;αC是齒輪 C 齒頂壓力角;αk 、αB 、 αC 計算公式如下:

式中:m 是齒輪模數;α 是變位之前的標準壓力角,取值為 20°;r′ 是齒輪 B 和齒輪 C 的實際中心距;dbC 和 dbB 分別是齒輪 C 和齒輪 B 的基圓直徑;daC 和 daB 分別是齒輪 C 和齒輪 B 的齒頂圓直徑。dbC , dbB,daC,daB 計算公式如下:
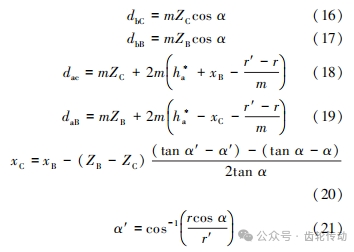
式中:h∗a 為齒頂高系數,取值為 1;xB ,xC 分別為齒輪 B、齒輪 C 的變位系數;r為理論中心距;r′ 為實際中心距;α′ 為變位后分度圓端面壓力角。
至此,綜合式(4)~ 式(19),3K 行星減速器齒輪系的嚙合效率計算公式中的已知量為:齒輪 A,B,C,D,E 的齒數 ZA,ZB ,ZC ,ZD,ZE;變位之前的標準壓力角 α;理論中心距 r;齒頂高系數 h∗a;齒輪模數 m;未知的變量為:實際中心距 a′;齒輪 B 變位系數 xB;齒輪 E 變位系數 xE 。
綜上,要使齒輪系嚙合效率最高,則需要選擇最優的中心距 a′ 和變位系數 xB 和 xE 。
3、減速器最大效率優化方法
由前述可知,在減速器的速比和尺寸根據設計需求已經確定的情況下,齒輪模數和各齒輪的齒數也已經確定,在此條件下,要使減速器齒輪傳動系統實現最大的嚙合效率,可以調整的變量只有三個:齒輪實際中心距 a′;齒輪 B 變位系數 xB、齒輪 E 變位系數 xE。
本文設計方案中的標準減速器參數如表 1,各齒輪均不變位。
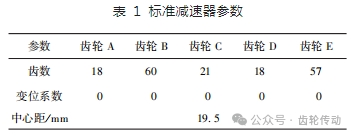
根據前述效率精確計算方法,按照標準減速器參數,計算得到的減速器嚙合效率為 78. 2%。
效率優化開始前,先根據減速器齒輪系設計原則和實際結構設計約束,確定中心距、齒輪 B 變位數、齒輪 C 變位系數可以變動的的范圍。本文方案中,中心距可變動范圍為 18. 5 ~ 20. 5 mm,齒輪 B 變位系數可變動范圍為-0. 7~1. 0,齒輪 E 變位系數可變動范圍為-0. 6~1. 0。
在中心距可變動范圍內,每間隔 0. 1 mm 進行一次齒輪效率的計算,在每個中心距下,齒輪 B 變位系數和齒輪 E 變位系數也間隔 0. 1 進行排列組合。本文方案中,中心距有 21 個可選值,每個中心距下,齒輪 B 和齒輪 E 的變位系數有 306 種組合, 一共能計算得到 6 426 個不同的排列組合,從中選出效率最大點對應的中心距、齒輪 B 變位系數、齒輪 E 變位系數。
表 2 為中心距為 20 mm 時的減速器嚙合效率數據,圖 3 為對應的嚙合效率圖。

在20 mm中心距情況下,當齒輪 B 變位系數為 1、齒輪 E 變位系數為 1 時,減速器嚙合效率最高為 86. 3%。以此類推,可以得出在中心距可變動范圍為 18. 5~20. 5 mm內,每間隔 0. 1 mm 中心距對應的最大效率,最后對選取所有中心距下最大效率值和對應的變位系數參數作為最終的設計參數。
本方案中,最終選擇得到的效率最優時的減速器參數如表 3 所示。當中心距等于 20 mm、齒輪 B 變位系數等于 1、齒輪 E 變位系數等于 1 時,效率最大為 86. 3%,最終設計采用改組參數作為減速器的設計參數。
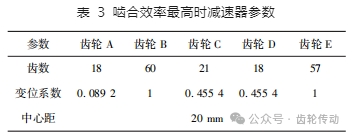
根據前述,按照標準減速器參數,計算得到的減速器嚙合效率為 78. 2%,比前述經過效率優化后的減速器嚙合效率 86. 3%低 8. 1%,說明經過效率優化后,減速器的理論嚙合效率有效提高。
計算得到減速器軸承系統效率 ηB 為 96%,攪油效率 ηS 為 97%,因此,最終減速器的傳動效率 η 為 80. 3%。

4、試驗驗證
根據前述效率優化后的減速器參數進行樣機設計,并進行減速器傳動效率測試,如圖 4 所示,用于減速器傳動效率測試的樣機為未裝入電機的模組。

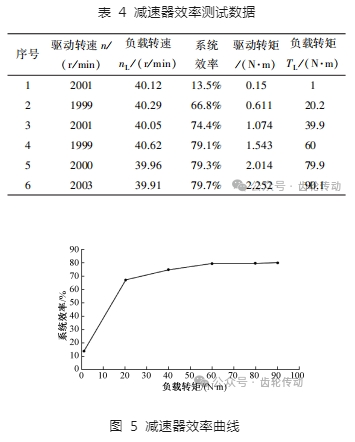
在額定載荷 90 N·m、額定輸入轉速2 000 r/ min 條件下,進行減速器效率測試,結果如表 4 和圖 5 所示。測得的最大傳動效率為 79. 7%,與前述減速器理論傳動效率 80. 3%接近。
5、結語
本文推導出了 3K 減速器精確的效率計算公式,并基于該公式提出了一種提高減速器嚙合效率的優化方法。
基于本文所提及的優化方法,進行了樣機的設計及測試,測試結果表明,該優化方法計算得到的減速器效率跟實測值吻合。
對于其他類型的齒輪減速器,也可以采用本文所提及的單對齒輪嚙合效率計算方法計算得出嚙合效率,并代入相應減速器效率計算公式進行減速器齒輪系嚙合效率的計算。
參考文獻略.
